Marching squares
Wikipedia has a good general description of the algorithm; here we focus on the specific case where input samples are binary (0/1, background/foreground, empty/full, water/land…)
Somewhat related: https://doc.mapeditor.org/en/stable/manual/terrain/
Coordinate system
Each cell is determined by its 4 corners -> N×N input produces (N-1)×(N-1) output cells
There are two possible interpretations of the input coordinate system; this makes no difference to the algorithm itself, it just changes how you would display the result.
Samples in cells corners
Grid and sample coordinates are integers.
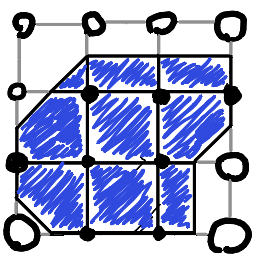
Like a heightmap, this requires an odd number of points for an even-sized grid and vice versa.
Samples in cell centers
This often makes sense in grid-based games/simulations, since the samples can directly determine properties of their corresponding cells.
Grid coordinates would normally be integers, while centers would be offset by 0.5 (but the converse is also possible, with the grid starting at -0.5).
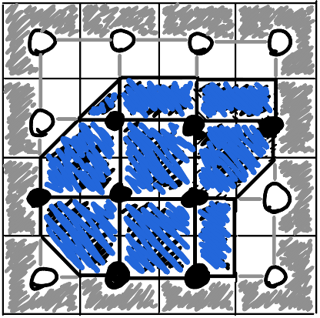
Grid size is unchanged, but a half-unit-wide border remains without data.
A possible workaround is to pad the input data with a fixed value on all 4 sides.
Ambiguity
Saddle points are ambiguous, in particular if input samples are binary. There are multiple conceivable strategies to resolving this:
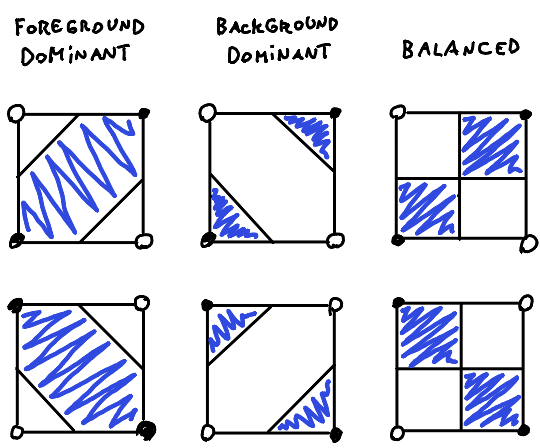
The simplest solution is to just choose one and stick to it (can also alternate based on x, y)
Indexing convention
For tile look-up, it’s useful to define a numbering convention, that is, a way of assigning indexes 0 to 15 to the 16 different combinations of corner values. The choice is completely arbitrary. I like the following one, since it is easy to remember:
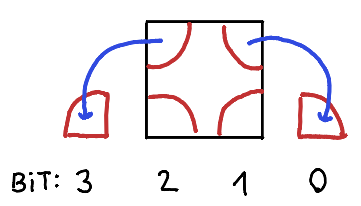
The tile look-up table then looks like this:
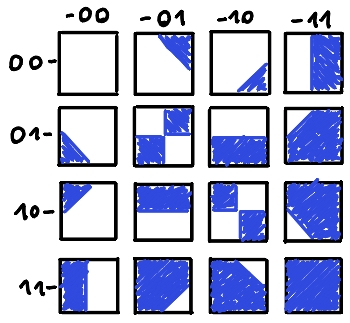
My implementation
In Tilevision: https://github.com/mcejp/tilevision/blob/41bbc61ff3e632a5084d55d8db73bea7498c9092/tilevision/path_util.py#L34 (note: uses a different indexing convention)